
三角形の面積比を解説 平面図形が苦手な人でもわかりやすい解き方 基本編 中学受験ナビ
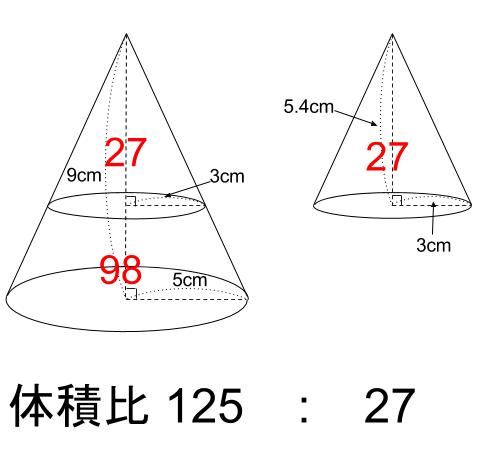
空間図形 相似な立体では 長さの比は相似比と同じ。 面積比は相似比の2乗。 体積比は相似比の3乗。 相似比がabの相似な図形の場合 辺、高さなど 長さの比は a b 表面積など 面積比は a 2 b 2 体積比は a 3 b 3 例 相似比23の相似な円柱PとQがある。 2h 2r 3r 3h『相似な図形』の単元の中から 平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので
比の求め方 図形
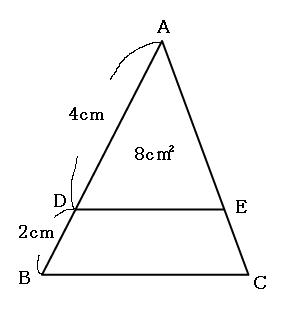
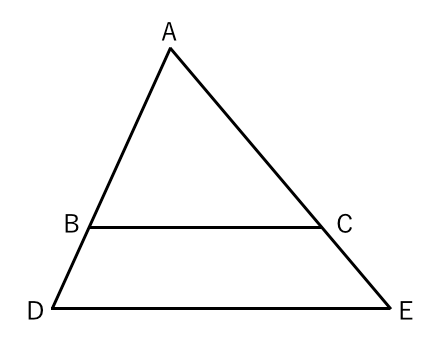
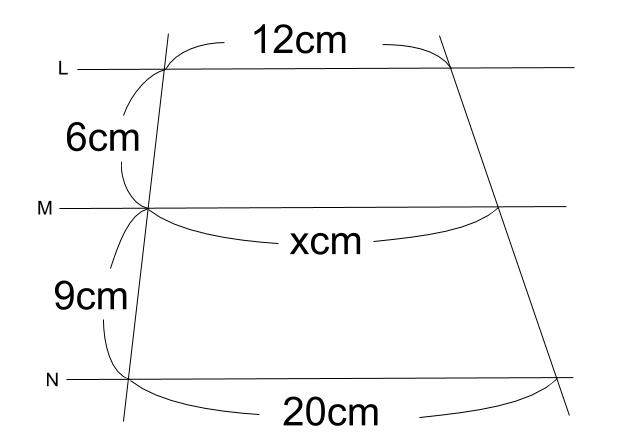
比の求め方 図形-平行線と線分の比の利用 平行線と線分の比を用いる問題を練習しましょう。 \(2\) つの似ている図の問題を比較して、平行線と線分の比の利用について理解を深めましょう。 例題1 次の図で、直線 \(L,M,N\) が平行のとき、\(x\) の値を求めなさい。 ① ② 解説相似な図形の場合、 相似比を2乗して面積比を作りましょう! 面積比が分かったら、あとは楽勝だね (^^) 図形Bの面積を とおいて、比例式を作っていきましょう。 よって、図形Bの面積は ㎠ となります。 相似比の2乗だ! ってことを覚えておけば簡単です
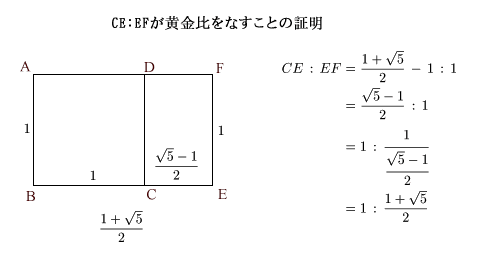
黄金比
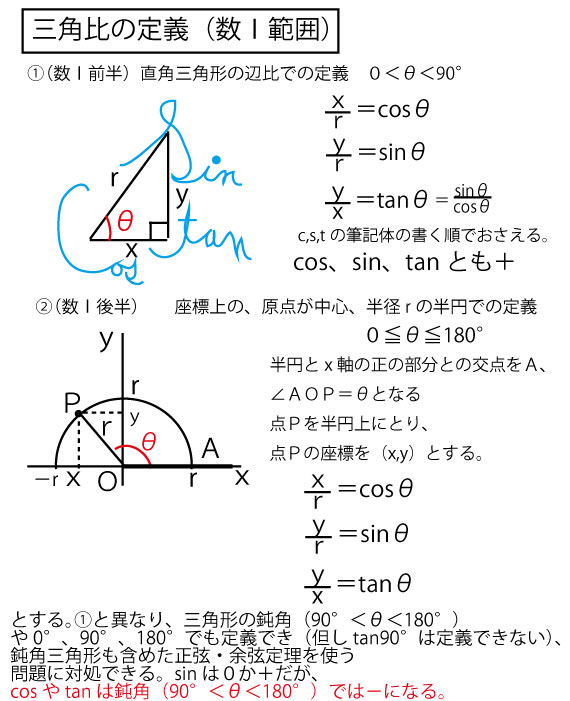
受験算数でも頻出の「平面図形と比」を取り上げます。 <問題1 (2)の考え方と答え> 次に、cr : rp : pd = 2 : 2 : 1 に注目して、 底辺比を着実に確認していけば、面積比は必ず求められますから、自分で図に比を書きこんで、早く慣れるようにし図形と計量90°θの三角比 図形と計量90°以上の角の三角比の値について 図形と計量cosの値が負になるときの角度の求め方 図形と計量sinを含む分数の式の計算方法 図形と計量sin,cos,tanの値の覚え方 図形と計量tanの値からcosの値を 前回 までの面積比問題の解き方は、イメージとしては内側の分割された図形から分析し、全体に迫っていくという流れでした。 つまり部分から全体に向かって攻めていたわけですが、今回学ぶアプローチは真逆です。 全体の面積がどのように分割されて
定義や公式(面積の求め方)、面積比の計算問題 この記事では、「台形」の定義や面積の公式、性質などをできるだけわかりやすく解説していきます。 計算問題も紹介していきますので、この記事を通してぜひマスターしてくださいね! 台形とは解説 ≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。 チェバの定理というのは、面積比と線分比の考え方の一部、ということなんじゃ トンちゃん なるほどです! といっても具体的に解説しないと、何言ってるかわかりにくいじゃろうから、 さっそく、具体的に解説をしていくかのぉ 目次 1 数学面積
比の求め方 図形のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 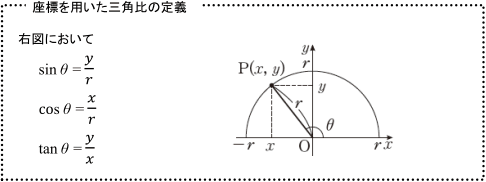 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 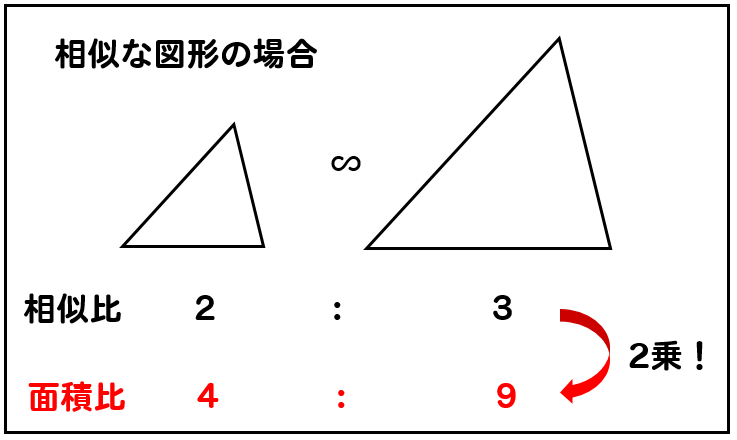 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 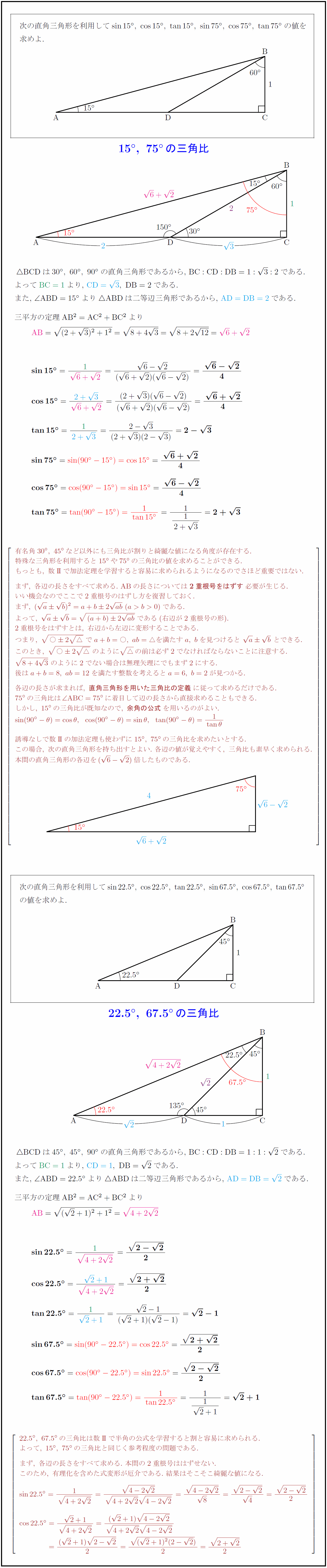 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 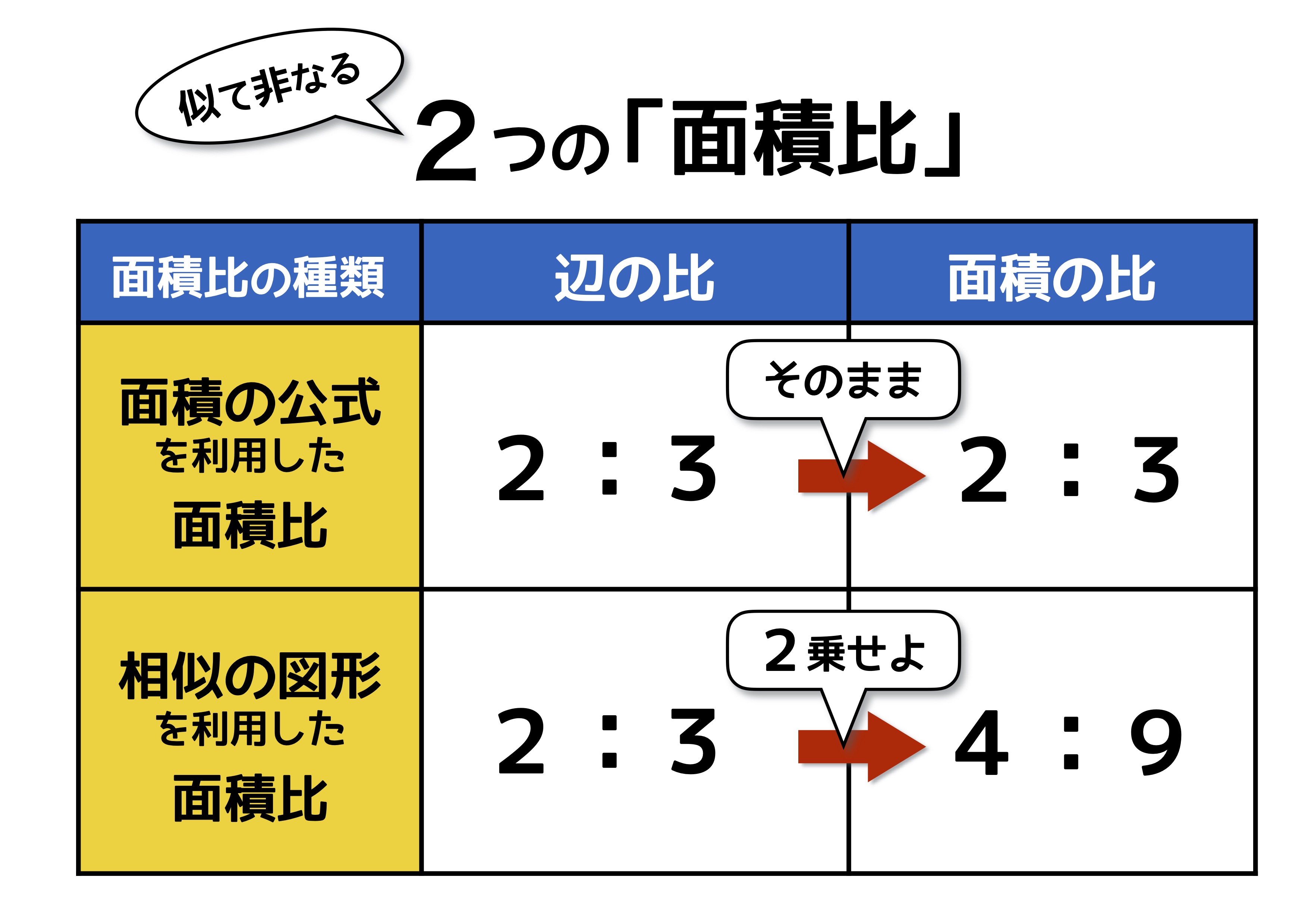 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 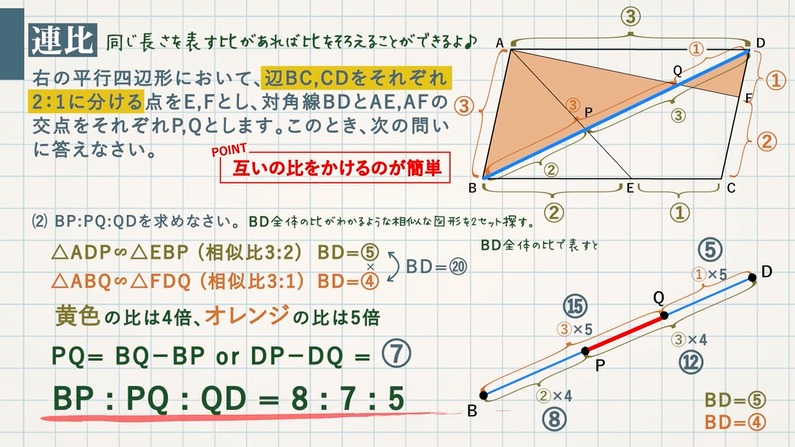 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 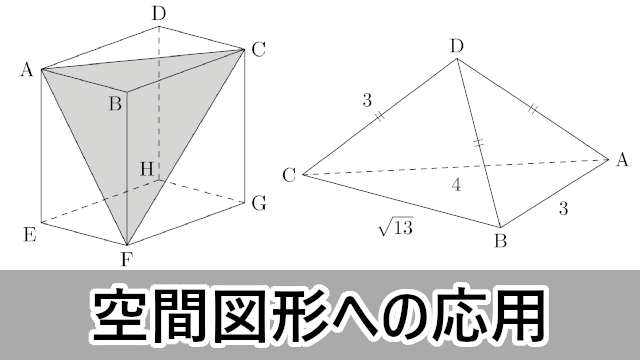 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 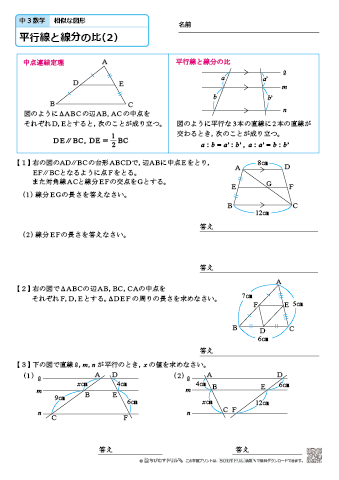 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 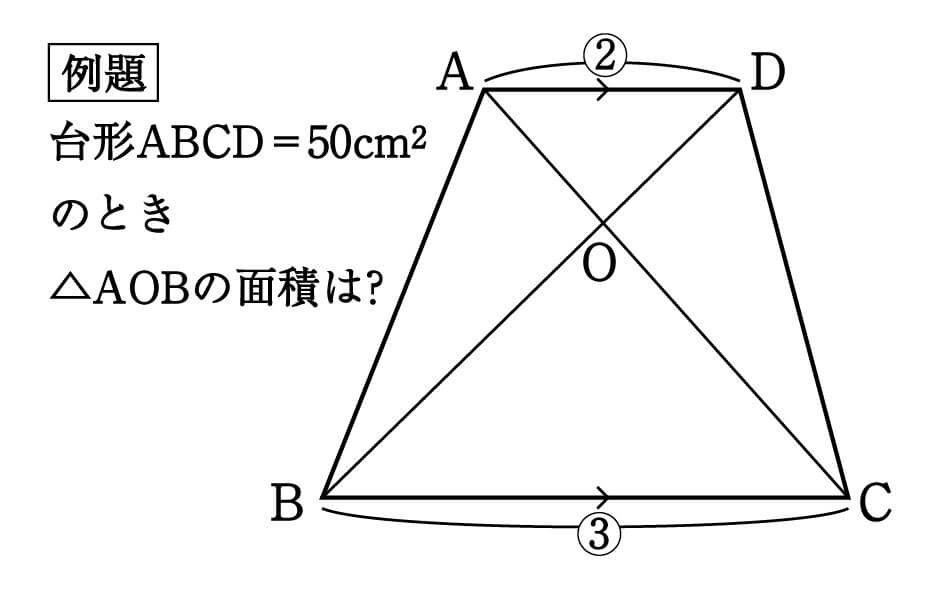 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 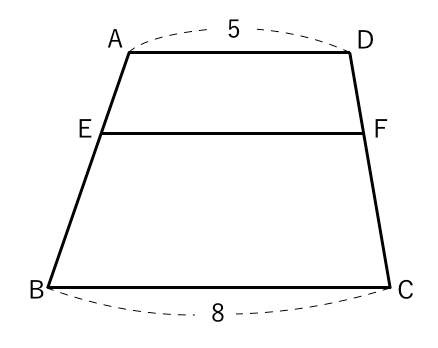 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
「比の求め方 図形」の画像ギャラリー、詳細は各画像をクリックしてください。
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 | 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
 90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |  90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座 |
こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がか また、ついでに $\sin 75^{\circ}$ も求めることができます。三角比の範囲では、これらの値を覚えておく必要はありませんが、「今の時点でこういう値も求められる」ということで紹介します。 なお、計算の途中で、基本二重根号の外し方の内容を使います。





0 件のコメント:
コメントを投稿