有効数字 問題 266511

例）100の有効数字は，1桁かもしれなし，3桁かもしれない．3桁の場合には，100 x 102 のように有効数字を明示する(規則(iii))． v) 有効数字の桁数は，単位の取り方とは無関係である． 例）117 mgの有効数字は3桁であるが，単位を変えて「 g」，「117 x 104 µg」有効数字 問1 次の数値は有効数字何桁の表記か答えよ。 ⑴ 12 ⑵ 1230 ⑶ ⑷ 10 ⑸ 123*104 問2 有効数字を考慮して，次の計算をせよ。 ⑴ 45 678 ⑵ 45 678 ⑶ 45 * 678 ⑷ 45 ÷ 678 例題2 解 答 問1 ⑴ 2 桁（問題） 次ぎの数値 a、b の積を答えよ。ただし、結果は ×10^nの形で答えよ。（10^nは10のn乗を意味する。） －－－－－－－－－－－ 結果の桁数は、四捨五入して、掛け合わせる数値の中で、有効数字の桁数が最も小さい桁と同じにする。 （または相対誤差の大きい測定値の有効数字より1

有効数字とはなんですか あと 写真のような問題は どう考えればよいですか Clear

有効数字 問題

有効数字 問題- 有効数字が分からん！ 問題を解いていけばいくほど気になる有効数字。 学校や塾の先生から「有効数字気をつけてね」とか言われるけど、良く分からない。 そんなあなたにお届けするページです。 初級編、中級編、上級編に分けてみました。 きちんとした説明は他サイトを参考にして 物理の問題で良く出てくる『 有効数字(ゆうこうすうじ) 』とは、「誤差が入っていても、測定値としての信頼性が高い桁の数字」のことでしたね。 (有効数字について詳しくは こちら) 物理では、精度良く測定値を求めるだけではなく、測定値を使って色々な計算をすることがありますね。

有効数字2桁で表せ という問題で 下の写真が解説なのですが答え方は6 0 10 11 Clear

有効数字とは、jis k0211により次のように定義されている。 「測定結果などを表わす数字のうちで位取りを示すだけのゼロを除いた意味のある数字」 有効数字とは、測定器で測定しうる量の有効な桁数の数字である。 有効数字には最小桁に誤差が含まれる問題に「有効数字2桁で答えよ」という指示がありますから，有効数字3桁目の2を四捨五入して，答えは「」となります。 有効数字の桁数を明らかにする場合，A×10 n の形を用います。Aは有効数字の部分です。 まず，指数について確認しておきましょう。 aをn個掛け合わせたものをaのn乗と問題の答えは分かっているものの、文章中にどう答えるべきかどうかが頭を悩ませる問題になるものです。 有効数字とは何か、そして文章中で答えるための方法について見ていきましょう。 有効数字について 有効数字とは自信を持って測れた数値を指しています。 仮に㎝までの長さの正確

有効数字 問1 次の数値は有効数字何桁の表記か答えよ。 ⑴ 12 ⑵ 1230 ⑶ ⑷ 10 ⑸ 123*10 Z会グループ公式サイト有効数字の説明と練習問題のページです。高校物理の通信教育ならZ会へ。難関大学に強いZ会で大学合格を目指す。 Keywords 物理,有効数字,受験,勉強,問題集,復習次のそれぞれの値を有効数字4けたで表わせ。 kg m km 次の測定値は何の位まで測定したものか。 735×10 2 g 210×10 3 m 500×10 3 km 2333×10 6 kg 299×10 7 l ×10 7 mm pdfファイル 解説ページに解説がない問題で、解説をご希望の場合はリクエストを送信してください。 解説リクエスト あくまで問題は「3951の答えを求めよ。」ではなく、「 3951を筆算（ひっさん）でしましょう。 」という小数を習いたての小学生に向けた筆算の練習問題。繰り上がりの1も書いてますよね。 有効数字(有効桁数)

 有効数字は問題文にでてくる一番少ないケタにあわせます 例;問題文に 1、245 0、2 3、47 という数値があったとき、答えをかくときは問題文の一番少ないケタ 0、2 つまり有効数字2ケタで答えます ナイス！ その他の回答をもっと見る練習問題：次の計算を有効数字を考えてせよ。 2 －2 です。 3．有効数字の足し算・引き算 足し算引き算の場合は、有効数字よりも位がポイントになります。 ポイント③：足し算・引き算では、計算結果を最も末位の高いものにあわせる。 ※それにより、有効数字の桁数が変わることがある。 4 有効数字の指数表示 高校物理では，有効数字の桁数が何桁なのかを分かりやすくするため，指数を用いて有効数字を表します。 大きい数字や小さい数字は 1桁目と2桁目の間に小数点が来るように表示 します。 ただし，有効数字の桁数は変えません

有効数字とは 化学の問題や計算で考え方をわかりやすく解説するよ 三重の個人契約家庭教師

問題文に有効数字2桁とか何も書かれてないのに 答えでは有効数字2桁で書かなくてはいけ Clear

有効数字 の考え方 981 は有効数字3 桁である。 実際問題の答え方 有効数字は意味を知っておく必要もあるが，どちらかというと理屈よりも問題の答え方に 神経を尖らせてほしい。計算結果が整数値で求まったときや割り切れたとき，また深い小数 になったときはつい忘れがちなので注意し 有効数字の桁数だけが重要になってくる 最も有効数字の桁数の小さな数値を見付け, 計算結果はその桁数と同じになるように記録する 次の例は有効数字が 3 桁と 2 桁の数値の掛け算だ 途中計算では何桁もの数字が並ぶだろうが, 結果は 2 桁で表す問題 Level1 mの有効数字は何桁か。 また，kgの有効数字は何桁か。 Level2 次の数字を有効数字2桁にせよ。 （1）4m （2）1375m/s （3）6218Hz （4）s （5）4πm 2 Level3 有効数字に注意して，次の計算をせよ。 （1）224×14 （2）340×10 22 ÷60×10 23 （3） （4）1755−1737 この下に

この問題の解き方を教えてください Clear

有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

最も大きいのは「32」の有効桁位=1位である。 (8) 計算結果を最大有効桁位に丸める。 443を有効桁位=1位に丸める。答えは「44」。 『練習問題』有効数字を考慮して以下の計算を行え。 (1) 784 055 = (2)有効数字を使った計算では、誤差が拡大したり不要な桁が増えたりしないように切り捨てを行いながら計算を進めます。 そして、最終的な答えを出すときに 四捨五入を行います。 今回の計算は，問題文に有効数字3桁で答えるよう指定されています。 な@ l @ Ȃ␔ w ł͗l ͂ 肳 邽 ߂ @ l p ̂Ƃ @3 ~10 2 @ l q ̂Ƃ @30 ~10 2 @ l r ̂Ƃ @300 ~10 2 @ ̂悤 ɕ\ ܂ d

中1数学 有効数字 例題編 映像授業のtry It トライイット

この問題分からないので教えてください 解き方だけでも良いです Clear

有効数字がどちらも3桁で、3桁の有効数字 21．7を答えとした。 （2）「有効数字 桁で答えよ」→途中計算は、 より1桁多く求めて、この桁で四捨五入して答える。 問題に指示がない場合は、 「計算する数値の中で最も桁数の少ない桁で答える」 5問題に有効数字の桁数について指示があった場合は，有効数字の桁数よりも1桁多い桁の数を四捨五入して有効数字の桁数にそろえます。 ≪「有効数字2桁で答えよ」と言われた場合の答え方≫ ご質問いただいた問題を例に，具体的に考えてみましょう。 この問題では，地球の全周lを計算すると$12$ は有効数字2桁 $1234$ は有効数字4桁 なので、 桁数が最小であるものの桁数 は、2桁です。 かけ算の結果は、正確に計算すると $$ ですが、2桁だけを残して（3桁目を四捨五入して）$15$ と表現するのが一般的です。

物理ネコ教室007有効数字とその意味 ひろじの物理ブログ ミオくんとなんでも科学探究隊

有効数字と指数の表し方について 理科 苦手解決q A 進研ゼミ高校講座

 有効数字は理系の問題を解くうえで非常に重要 です。 大学受験においては、特に化学では、有効数字を使った問題がよく出題 されます。 数学に関しては、大学受験で有効数字を気にしなければならない問題はあまりありませんが、大学の理系学部では知っておかなければなりません。有効数字 01cmの目盛りがついたものさしで長さを測り，測定値（近似値）が37cmだったとき，こ の近似値の37という数字は信頼できる。 このような信頼できる値のことを有効数字という。 有効数字 そこで今回は計算問題の中でも有効数字に注目して解説していこうと思います 解説だけでなくアウトプットもできるように練習問題も用意しました 有効数字について 有効数字とは;

中学１年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

物理基礎での有効数字について教えて下さい 2 の答えはなぜ小数第 Yahoo 知恵袋

有効数字について 有効数字2桁で答えろという問題で、 015×10^23と 15×10^22では どっちが正しいですか？ 化学 この問題解ける人いますか？各問題の注意 (1) 有効数字3桁の最終桁は小数2位の9である。それ以下がそのちょうど半分(0005)であるから五捨五入を行う。9は奇数であるから切り上げる。小数2位の0は必要。 (2) 問題(1)と同様に有効数字3桁の最終桁は小数4位の9で、五捨五入を行う。数値の丸め方 練習問題 (1) を有効数字 3 桁に丸める 《解説》 (2) 737 を小数第 1 位までに丸める 《解説》 (3) を有効数字 3 桁に

この問題の の答えの有効数字の求め方について聞きたいのですが なぜ有効数字2桁の1 Clear

中1数学 有効数字の求め方のポイント 練習問題 Pikuu

問題 難易度★☆☆☆☆（易しい） 次の(1)～(5)は，計測の結果，得られた測定値を用いた計算である。これらのうち，有効数字と単位の取り扱い方がともに正しいものを一つ選べ。 \\begin{eqnarray}加減算の精度 練習問題 電卓を使って左辺の計算をしたところ，右辺の結果が表示された。有効数字を考慮して答えを示せ。数値はすべて測定値であるものとする。 (1) \(53 = \) 《解説 有効数字の問題例 3人の生徒が異なるスケールを使用してアイテムの重量を量ります。 これらは彼らが報告する値です： a。03 gb 。0 gc 。003 kg どのように多くの重要な数字は各測定で想定すべきですか？ 解決 a。4 B。3小数点以下のゼロは、アイテムの重量が01gに最も近いことを示し

有効数字についての質問です この反応速度を求める問題で有効数字2桁で答えろと言われて Clear

物理の有効数字について この問題の答えが 2 M S になっ Yahoo 知恵袋

 誤差と有効数字、近似値の表し方の問題です。高校の理科でも使う分野なので、教科書でしっかり意味を確認してから問題に取り組んでください。誤差とは、真の値と近似値との間にある違い、つまり、誤差＝近似値－真の値です。例）測定値 505kg 真の値 502kg のとき 505kgー502kg＝03kgが誤差 \( = 385 \quad \to \quad 39\) (理由) 精度の高い位に合わせても、それ以上悪い位がかき消すほど誤差が大きいからです。 極端な事を言うと、\(① \pm\)の（精度の良い）誤差があっても、\(②1\pm10\)の（精度の悪い）誤差を足し合うと、①の（精度の良い）誤差が無意味な事が分かり有効数字 3 桁 70 有効数字 4 桁 0007 有効数字 3 桁 × 10 3 有効数字 2 桁 700 おそらく有効数字 3 桁 だが、 4 桁とも 5 桁とも取れる (他の数値との比較などから判断) 有効数字をはっきり示したい場合は 7 × 10 4 (3 桁の場合)のような表記法を用いる

有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

電験における有効数字の取り扱い 電験3 1種合格者が解説 いちにょきブログ

有効数字 の 有効 とは コンピュータの計算などでも問題になる注意すべき例である また, 3つめの式のように有効数字の桁数が2桁の二つの数から有効数字3桁の数が生じることもある このように, 有効数字の和差計算では有効数字の桁数が増減する可能性がある 測定値同士の乗除計算 測定有効数字の桁数が多いものほど，より正確に測定したということです。 有効数字の桁数の数え方 問題を解いていると「有効数字 桁で答えなさい」という問題に遭遇します。 この問題に正しく答えるためには，まず有効数字の桁数の数え方を知る必要が

2

モル濃度の問題ですが 1 はなぜ有効数字が3桁になるのでしょうか 1 8gの2桁が Clear

虚数 東工大化学第9問 この問題って有効数字3桁じゃないんかな Twitterの非公式解答速報見ると全て有効数字二桁なんだけど 東工大 東工大化学

有効数字の問題です 有効数字の途中計算はn 1桁まで求めて最終的に四捨五入してn桁に Clear

単位変換 有効数字の計算問題 ガッコン 学習コンサルタント Note

この問題の 2 って10 0何ですが有効数字３桁っておかしくないですか 物理学 教えて Goo

物理基礎の有効数字の問題で 測定値同士の足し算 引き算は1番下のくらいが Yahoo 知恵袋

有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

有効数字って何 計算方法や桁数の求め方を詳しく解説します

高校物理でこの問題なんですが 問題に書いてある数値は全て有効数字2桁や3 Yahoo 知恵袋

Studydoctor有効数字とは 表し方 中学１年数学 Studydoctor

この問題は有効数字2桁で答えるのですが25 10でも有効数字2桁ではないのですか Clear

この問題の場合有効数字って何桁になりますか また理由も教えてくださ 物理学 教えて Goo

有効数字2桁で表せ という問題で 下の写真が解説なのですが答え方は6 0 10 11 Clear

有効数字とはなんですか あと 写真のような問題は どう考えればよいですか Clear

中1数学 有効数字 近似値と誤差の要点と定期テスト対策問題 Examee

2 の問題ですが 有効数字2桁をかけているのに答えは有効数字3桁になっているのはな Clear

問題文に使われている数字は全て有効数字3桁なのに 何故青丸の答えは有効数字2桁なので Clear

中学１年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中学数学 有効数字の1つの計算方法と考え方 Qikeru 学びを楽しくわかりやすく

有効数字は問題文の一番小さい桁数ですが今回9度が一番小さい桁数ですがなぜ答えは1桁で Clear

有効数字の質問です 化学の問題を解く時 有効数字の指定がある場合有効数 Yahoo 知恵袋

中学１年生 数学 資料の活用 近似値と有効数字 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

この問題の の答えが5 10 4mol Lなのですが これは有効数字が整数までであ Clear

030 化学基礎 有効数字の定義 数え方 加減乗除の解説と実践的な化学での問題実践 Youtube

有効数字 有効桁数

この問題の有効数字の合わせ方が分かりません 先生には最初に立てた 物理学 教えて Goo

物理基礎について 有効数字について 写真の問題30です 私は19 6m 物理学 教えて Goo

計算問題における有効数字と四捨五入の扱い 電験１種の棚卸し

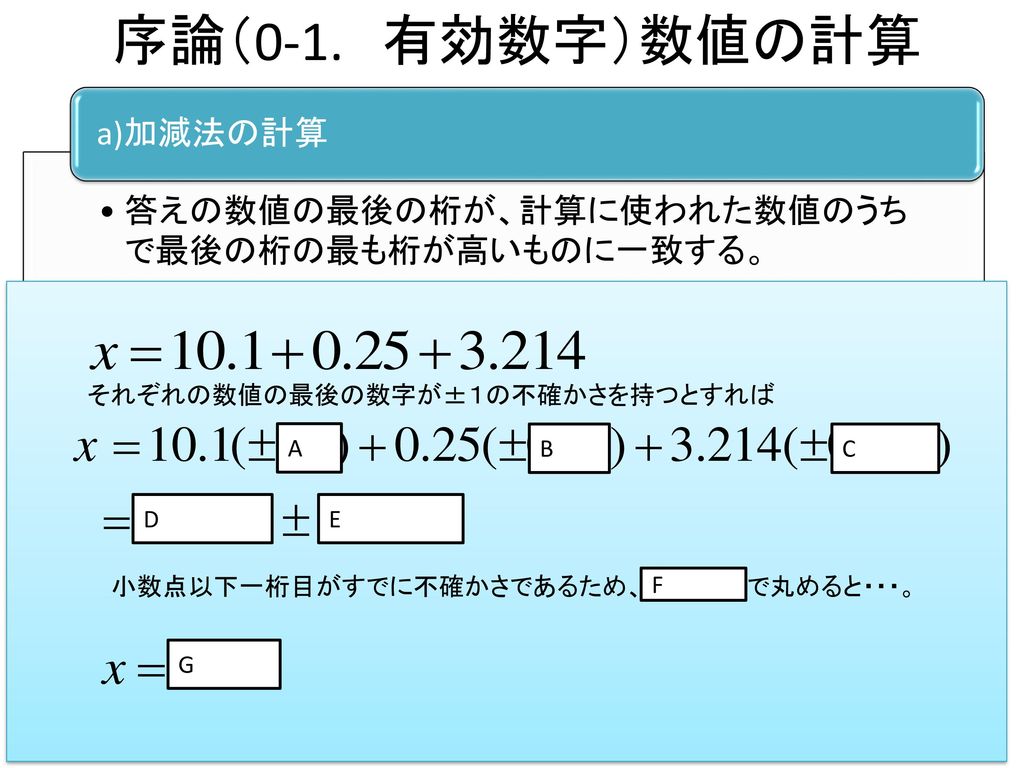
学年 名列 名前 福井工業大学 工学部 環境生命化学科 原 道寛 名列番号 氏名 Ppt Download

有効数字の問題です 有効数字の途中計算はn 1桁まで求めて最終的に四捨五入してn桁に Clear

問題文は有効数字2桁で書いてあるので答えも2桁で書かなければ Yahoo 知恵袋

有効数字

この問題は有効数字二桁ではないんですか Clear

有効数字を考慮するって どういう意味ですか 調べても 納得す Yahoo 知恵袋

有効数字の桁数の決め方 小数は位取りの0に注意 Dr あゆみの物理教室

有効数字の問題です なぜ0 65ではなく0 64になるのですか 有効数字 高校 教えて Goo

物理の有効数字について 写真の問題の 2 の答えの2m Sというのは Yahoo 知恵袋

有効数字と物理量の表しかたと端数の処理 Life Chemistry

この問題文には有効数字が2桁までしかありませんがなぜ答えの有効数字が3桁なんで Yahoo 知恵袋

資料の活用 Clear

電験どうでしょう H29 問14

有効数字と物理量の表しかたと端数の処理 Life Chemistry

第7 2回 有効数字の計算方法 四則演算 ばけぴとの分析化学講座

近似値と有効数字 教遊者

有効数字とは 物理で必須の掛け算や四捨五入の仕方を解説

Ptimes10q Descubre Como Resolverlo En Qanda

高校物理基礎有効数字の問題 何回か解いていますが 中々苦手で解 Yahoo 知恵袋

有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

化学の有効数字についてなんですが 問題文には2 0という１番小さい二桁があるの Yahoo 知恵袋

化学 この問題で文章中では有効数字3桁なのに塩素の分子量は2桁で計算 化学 教えて Goo

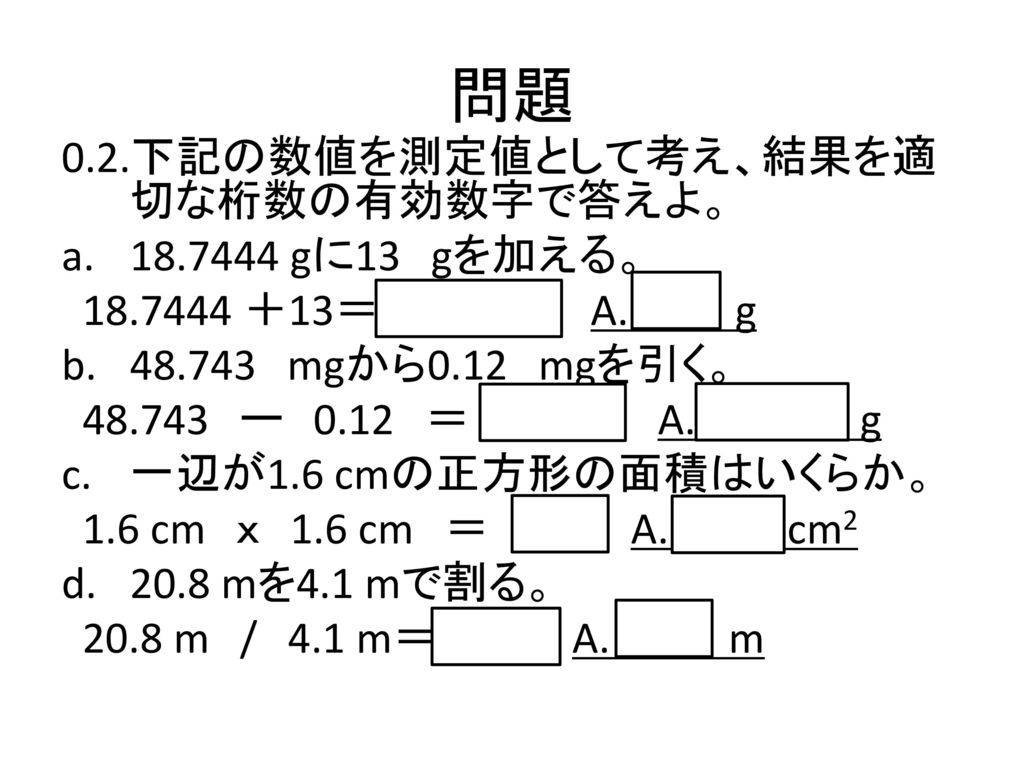
学年 名列 名前 福井工業大学 工学部 環境生命化学科 原 道寛 名列番号 氏名 Ppt Download

3

3

有効数字の問題でなぜ0 90と3桁で表すのですか なぜ0 9という2桁ではない Yahoo 知恵袋

有効数字二桁で答えよと言う問題なんですけど どっちが正しいのでしょうか Yahoo 知恵袋

地球の概観と構造 有効数字と指数の表し方について 地学基礎 定期テスト対策サイト

高一の物理の質問なのですが有効数字をいつ使えば良いか分かりません 宜しけれ Yahoo 知恵袋

この問題の問1の答えの有効数字は3桁ですか そうです 3桁同士の割 Yahoo 知恵袋

有効数字の問題に慣れよう 苦手な数学を簡単に

中1数学 有効数字 例題編 映像授業のtry It トライイット

有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

この問題の場合 答えは0 2ではダメですか 有効数字とか関係してますか Clear

1

物理基礎有効数字 の問題なんですけど問題文の有効数字が二桁ですが 答えは四 Yahoo 知恵袋

有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

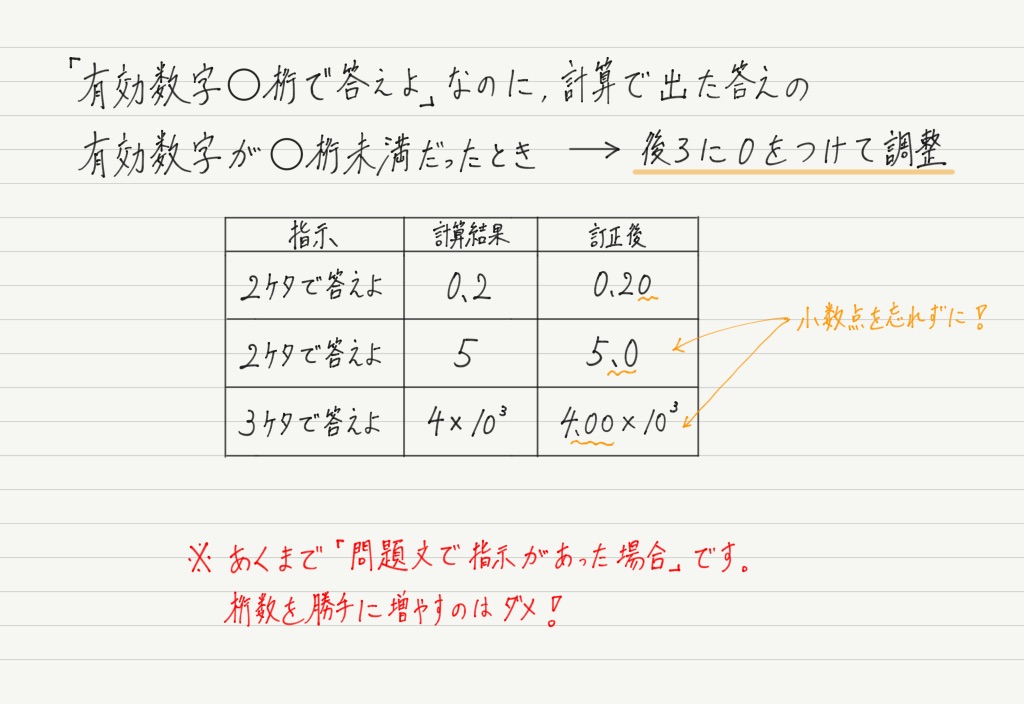
有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

問題文は有効数字2桁で書いてあるので答えも2桁で書かなければいけないと思うのですが書 Clear

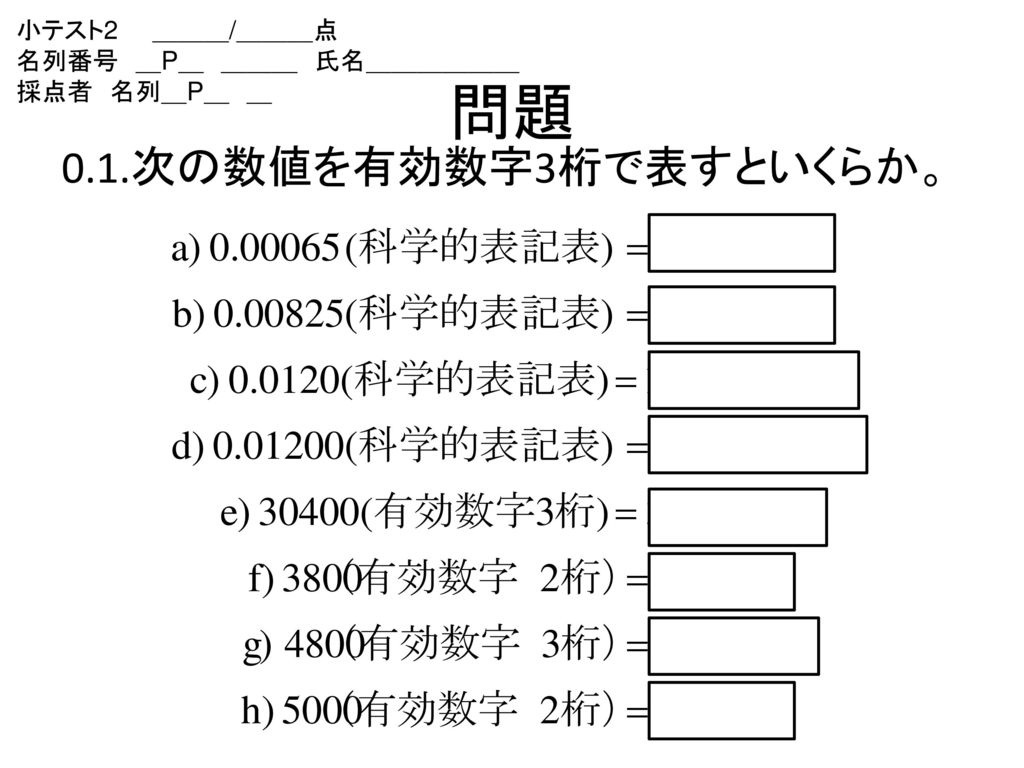
学年 名列 名前 福井工業大学 工学部 環境生命化学科 原 道寛 名列番号 氏名 Ppt Download

近似値と有効数字 教遊者

物理の有効数字について質問です 参考書は理解しやすい物理です例 Yahoo 知恵袋

四則演算による有効数字の桁数の変化 計算ルールを解説 Dr あゆみの物理教室

高校1年生 物理基礎の序章 指数と有効数字の問題です 6 の Yahoo 知恵袋

有効数字の問題です 6 0 24 30 0ですか 理由も教えてください Quora

中３数学 平方根 近似値と有効数字 問題 Youtube

この化学の問題なのですが 有効数字は問題中では3桁ですが 最 Yahoo 知恵袋

薬剤師国家試験対策 練習問題つき 有効数字について超丁寧に解説

物理基礎の問題で有効数字は二桁とするって書いてあって計算結果932 8 大学受験 教えて Goo

コース 有効数字 誤差の伝搬ー正式版 応用問題

2 の答えが19 6mで 計算は出来たのですが どうして有効数字3桁なのかが分かり Clear

この問題は有効数字二桁ではないんですか Clear

至急高校物理基礎有効数字の問題 有効数字の問題が苦手でテスト前 Yahoo 知恵袋

1

中学数学 有効数字の1つの計算方法と考え方 Qikeru 学びを楽しくわかりやすく

3分間で見る物理基礎 有効数字編 Youtube

有効数字 高校物理をあきらめる前に 高校物理をあきらめる前に

有効数字の桁に注意して 次の計算をしなさい 単位は省略しています 物理学 教えて Goo