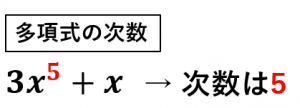
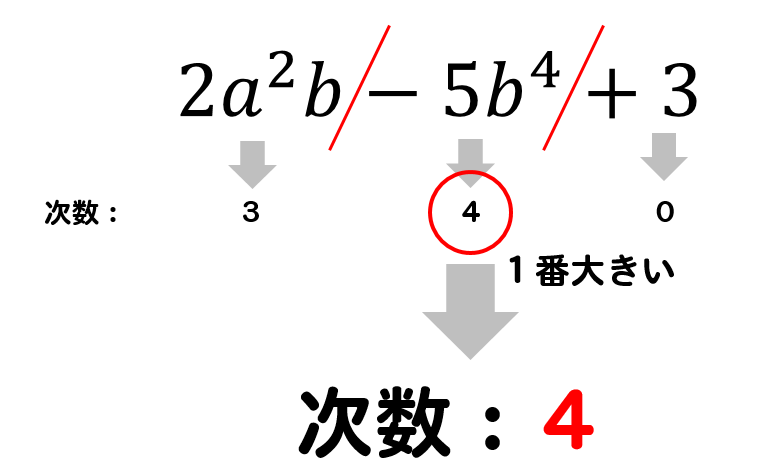
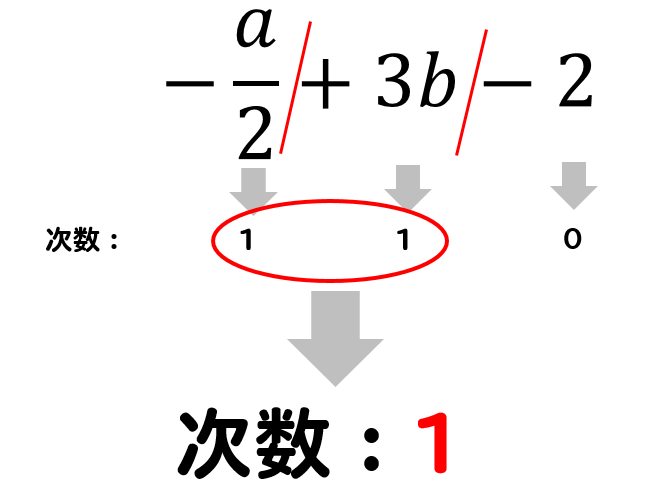
単項式についての用語の定義 単項式の数の部分を 係数 と言います。また,単項式において,かけられている文字の個数をその単項式の 次数 と言います。 例えば, 2 x 3 y z 2 2x^3y z^2 2 x 3 y z 2 という単項式においては, 2 2 2 が係数です。次数について 単項式,多項式どちらの場合でも, 次数が1の式 → 1次式 次数が2の式 → 2次式 といいます。 ちょこっと豆知識💡 1年生の時に1次方程式を習いましたね? これは,次数が1の式でつくられた方程式という意味 なのです。★単項式の次数・・・かけ合わされた文字の個数 2 の次数は, が2個なので,「2」 2 の次数は, が2個, が1個, が1個なので,「4」 ★多項式の次数・・・各項の次数の中で,もっとも大きいもの 3 2の次数は,「1」 (次数1) 2 − 2の次数は,「2」

単項式 多項式 何次式 係数 次数の見分け方を解説 数スタ
単項式 次数 意味
単項式 次数 意味-単項式 では、かけ合わされている文字の個数がそのままその単項式の次数です。 多項式 では、各項の次数のうちでもっとも大きいものがその多項式の次数になります。 多項式は何次の式かすぐわかるように,次数の高い順に項を並べて書くのが基本です。 例 2 x y 2 2xy^2 2 x y 2 の係数は 2 2 2 ,次数は 3 3 3 。 多項式 単項式の複数(2つ以上)の和として表される式のこと。 例 x 3 x3 x 3 , x 2 y 2 z 2 x^2y^2z^2 x 2 y 2 z 2 , 1 x x 2 x 3 1xx^2x^3 1 x x 2 x 3 整式 単項式と多項式を合わせて整式と言います



次数の意味 単項式 多項式 特定の文字に着目 具体例で学ぶ数学
関係用語として、単項式、多項式、係数の意味を勉強すると良いでしょう。下記が参考になります。 係数とは?1分でわかる意味、求め方、計算、多項式、単項式の関係 単項式とは?1分でわかる意味、係数、次数、項、多項式との違い 多項式とは? 次数とは? 単項式と多項式の回で、単項式とは数や文字をかけあわせて出来ている式のことだと勉強しました。 このかけあわせている文字の個数を、単項式の次数といいます。 例えば の場合、この単項式の中に含まれている文字の個数は が1つだけなので次数は1となります。単項式 単項式 とは,数や文字だけの積の形で表された式のこと. 例 5 a x 3 , − 2 b 2 y 4 単項式の係数と次数 単項式 において,その数の部分を 係数 ,かけ合せた文字の個数を 次数 という. 例 5 a x 3 の係数は5で次数は4となる. − 2 b 2 y 4 の係数は-2
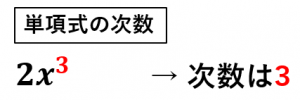
次数、〇次式とは? 次数(じすう)とは、 かけあわされている文字の個数 のことをいいます。 そして、次数が2である式を2次式、次数が3である式を3次式といいます。 ⇒ 単項式と多項式の違いは?「単」と「多」の違いを理解すれば簡単だ! 多項式の次数 ここまでは、単項式の次数について見てきました。 では、多項式の次数はどうでしょうか。 次の式を見てください。 $$7x^2x7$$ この式は引き算が使われているので、多項式ですね。 この多項式は以下の3つの単項式から作られています。単項式・多項式・次数 単項式と多項式 問題(1 学期中間) 次のそれぞれの式を単項式と多項式に分け,記号で答えよ。 ア 2a 4b 12 イ−5xy ウ − エ 3 2 −5x 2 解答欄 単項式:
数だけの単項式の次数は0とします. 高校数学Ⅱで x 0 =1 ということを習います.これにより, 3=3x 0 , 5=5x 0 と考えれば納得できるでしょう. ただし, 0x 3 , 0x 2 , 0x, 0 などは,いずれも単に 0 と書くので,数の 0 だけは次数を定めません.単項式と多項式とは ・単項式とは、文字や数字をかけ合わせて作られている式 ・多項式とは、単項式の和として表される式 従って、下の表のように分類できるよ。次数 1 単項式の次数 数と文字の積の形の式を単項式といい,かけ合わされている 文字の個数を,その式の次数という。 単項式5a,8xy,−x2y の次数を求めてみよう。 5a = 5 × a だから,次数は1 8xy = 8 × x × y だから,次数は2 −x2y = −1 × x × x × y だから,次数は3 次数が1 の式を1 次式,次数が2 の



1




中学2年数学 式の計算 単項式と多項式とは その次数と係数もマスターしよう 数学の面白いこと 役に立つことをまとめたサイト
単項式と多項式の違いは、その字のとおりです。 すなわち単項式は 2y、-5a などの項が1つの式です。 多項式は 3-2x+3a などの項が2つ以上ある式です。 次数の意味 のちのちのことを考えると「次数」という用語をしっかり把握しておく必要があります。多項式の次数 多項式は単項式の和として表される式のこと。 整式において、最も次数の高い項の次数をこの整式の次数といいます。 (例)7x ² 8x‐3は 2 次式 2x²3x ² y ²5y²は 4 次式 ・定数項111 整式 単項式と多項式 2,x,3a 2 , (5)x 2 yのように,数や文字、およびそれらを掛け合わせて出来る式を 単項式 という。 単項式において,数の部分をその単項式の 係数 といい,掛け合わせた文字の個数をその単項式の 次数 という。 2,5など,数だけの




3分で分かる 単項式とは 単項式とその次数 係数などについてわかりやすく 合格サプリ




文字式の重要な用語解説 単項式 多項式 項 同類項 定数項 係数 次数 数学fun
単項式と多項式の用語 単項式・多項式には、いくつかの重要な用語があります。 ここでは「\(2x^2 3x 1\)」という多項式を例に、「次数」「係数」「定数項」「昇べきの順」「降べきの順」の \(5\) つの用語を説明していきます。単項式の次数 単項式の次数は、変数のすべての冪指数(指数が書かれない変数の指数は 1 と考える)の和として定義される。例えば、 x a y b z c の次数は a b c である。より具体的に、 xyz 2 の次数は 1 1 2 = 4 である。単項式の次数 編集 単項式の次数は、変数のすべての冪指数(指数が書かれない変数の指数は 1 と考える)の和として定義される。例えば、 x a y b z c の次数は a b c である。より具体的に、 xyz 2 の次数は 1 1 2 = 4 である。




次数の意味 単項式 多項式 特定の文字に着目 具体例で学ぶ数学



中学2年数学 式の計算 単項式と多項式とは その次数と係数もマスターしよう 数学の面白いこと 役に立つことをまとめたサイト
単項式と多項式の項と次数|中学数学 数字と文字をかけた式を単項式、いくつかの単項式を足したり引いたりしたものを多項式といいます。 例 式 2a 単項式 7h 単項式 3x 2式の次数 Q 次の単項式を,乗法の記号×を使って表しましょう。 (1)2x ( ) (2)3x2 ( ) (3)5x2y ( ) 問1次の にあてはまることばを入れましょう。 単項式で,かけ合わされている文字の個数を,その単項式の次数単項式の次数 単項式の次数は、変数のすべての冪指数(指数が書かれない変数の指数は 1 と考える)の和として定義される。例えば、 x a y b z c の次数は a b c である。より具体的に、 xyz 2 の次数は 1 1 2 = 4 である。




文字式の計算



Math Tube 数 1 1 単項式の次数と係数 多項式の次数 Video Dailymotion
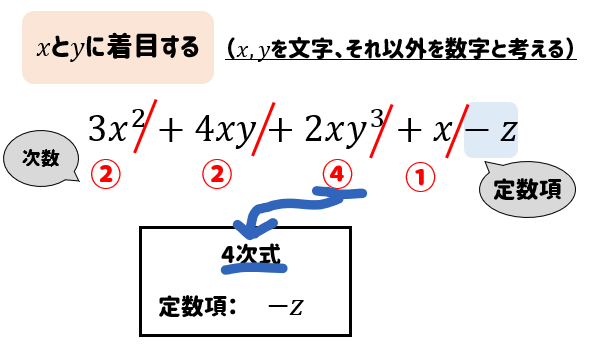
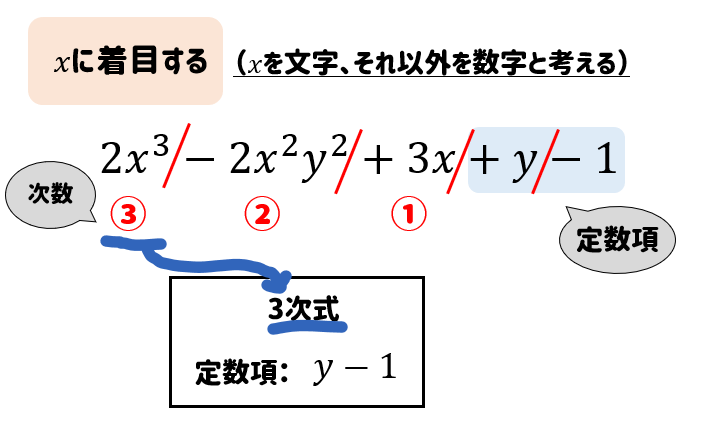
単項式が2種類以上の文字を含むとき、特定の文字に着目して係数や次数を考えることができる。 この時、残りの文字は数とみなして扱う。 例2 12 a b 4 x {\displaystyle 12ab^{4}x}まずは次数から確認していこう。 次数 は、ざっくりいうと 「文字が何個あるか」 を表すよ。 例えば、3x 2 の次数は2になるね。 (x 2 =x×xでxが2個) 例 3x 2 次数は2 単項式の場合は、 文字の右肩の数字が次数を表す よね。単項式であっても着目する文字によって次数が異なることがあります. x の単項式,及び,いくつかのx の単項式の和の形の式を,x(について)の といいます.多項式を構成する各々の単項式をその多項式の (term) といいます. 多項式の項の中で次数が最大




高校数学 単項式の係数と次数 練習編 映像授業のtry It トライイット




数学 単項式の次数と係数の求め方とコツ 教科書より詳しい高校数学
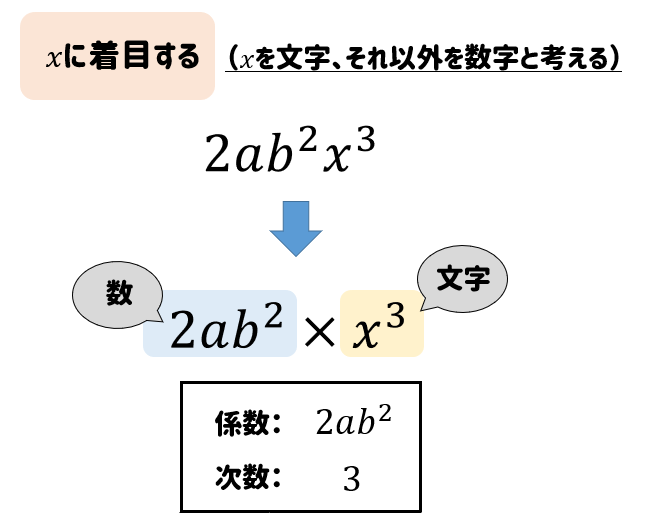
前回は、「係数」と「次数」のお勉強をしましたが、 この「次数」に関しては、 この式は 何次式? なんて聞かれることもあります。 これを答えるためには 「次数」が大切なので、 もう一度「次数」の説明していきます。 次数はどうやって数えるの?単項式のかけ算 係数をかけ算し、次数を足し算します。 例えば、$3x^2\times 2x^3=6x^5$、$2xy\times 3y^2z=6xy^3z$ です。 単項式のわり算 係数をわり算し、次数を引き算します。 例えば、$6x^5\div 2x^2=3x^3$、$2xyz\div 2x=yz$ です。 次回は 次数の意味(単項式、多項式単項式において、数の部分を係数 (coefficien) といい、掛け合わせる文字の個数を次数 (degree) という。 たとえば、$3abx^2$ の係数は $3$ で、次数は $4$ である(右図参照)。




高校数学 単項式の係数と次数 映像授業のtry It トライイット



高校数学 文字に着目したときの次数 係数の求め方は 数スタ
続いては次数について確認していきましょう。 単項式 では、 かけ合わされている文字の個数 をその式の 次数 といいます。 例: $2a$ , $5x$ → 次数 $\textcolor{blue}{1}$ $4ab$ , $3x^2$ → 次数 $\textcolor{blue}{2}$ それでは 多項式の次数 はどうなるでしょうか。 多項式では、各項の次数のうち、 いちばん 単項式は掛け算だけの式で、 単項式を足すと多項式になります。 ここからは単項式、多項式と一緒に覚えてもらいたい言葉を 紹介します。 項、係数、次数 項 多項式の中の単項式の部分 例 係数 文字を含む単項式の数字の値 例 次数 単項式の場合文字式の重要な用語解説(単項式・多項式・項・同類項・定数項・係数・次数) 管理人 12月 19, 18 中学校数学で習う文字式では重要な用語がいくつかでてきます。 これまで小学校で習ってきた算数などでは用語自体を意識して覚える必要があまりなかっ




単項式 多項式 何次式 係数 次数の見分け方を解説 数スタ




単項式 多項式 何次式 係数 次数の見分け方を解説 数スタ
単項式の次数 数や文字についての乗法だけでできている式を 単項式 といいます。 $$3x, 4ab, 2a^5, \frac{2}{3}$$ このように項が1つしかない式が単項式ですね。単項式の係数と次数 単項式の数の部分を係数といいます。ただし、 1x のように係数が 1 のときは省略して x と表されるので、 x の係数は 1 です。 同様にして、 −1a のように係数が −1 のときは省略して −a と表されるので、 −a の係数は −1 です。学習内容単項式 次数 係数この動画を見れば単項式、次数、係数がバッチリになります。単項式 次数 係数とは数といくつかの文字の積で




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ




中2数学 単項式と多項式 次数と次式 画像追加 Education Unbeatable
単項式の次数と係数 単項式 3、4a、-2x、a³のように、数字、または数字と文字を掛け合わせてできる式のことを、単項式と言います。 次数 単項式において、掛け合わせた文字の数のことを次数と言います。 "4a"の次数は、(掛け




単項式




どうしてこうなるのかが分かりません 解説お願いします Clear




単項式 多項式と次数 ときどき係数 教遊者




単項式




多項式 数学i フリー教材開発コミュニティ Ftext




3分で分かる 単項式とは 単項式とその次数 係数などについてわかりやすく 合格サプリ



この単項式 多項式 次数の意味がよくわかりません 教えて Yahoo 知恵袋



1




多項式と単項式の違いとは 次数や乗除 乗法除法 や分配法則についても解説 遊ぶ数学




係数 次数 問題




単項式 多項式と次数 ときどき係数 教遊者




Tsbe2exol9mqhm




単項式 多項式 何次式 係数 次数の見分け方を解説 数スタ



高校数学 文字に着目したときの次数 係数の求め方は 数スタ




単項式 多項式や次数 係数などの定義と問題例 高校数学の美しい物語



高校数学 文字に着目したときの次数 係数の求め方は 数スタ




多項式と単項式の違いとは 次数や乗除 乗法除法 や分配法則についても解説 遊ぶ数学




数学i 式の計算 1 1 単項式の次数と係数 Youtube




数学 単項式 多項式の次数 係数が分かる コツは一つの文字に注目すること ますmath数学を好きになる




1研究中 C 数学5 単項式 多項式 整式 分数式 有理式 無理式 係数 項の次数次式元




単項式 多項式と次数 ときどき係数 教遊者




式の計算 単項式と多項式の次数の数え方 中学数学 定期テスト対策サイト




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ



単項式 多項式 何次式 係数 次数の見分け方を解説 数スタ




単項式と多項式




3分で分かる 単項式とは 単項式とその次数 係数などについてわかりやすく 合格サプリ




Left 2right B Right Descubre Como Resolverlo En Qanda



2




例題 単項式の次数と係数 Youtube




中2数学 単項式と多項式 次数と次式 画像追加 Education Unbeatable




高校数学 多項式の次数 練習編 映像授業のtry It トライイット




中2 式の計算 単項式 多項式と次数 ときどき係数 デジタル板書データ Youtube



1




Xに着目すると二乗になっていても着目できるのですか Clear




多項式について 中学数学であいまいな点をはっきりさせよう 身勝手な主張



多項式と単項式とは 項 次数 係数などの意味や計算問題 受験辞典



3




Descubre Como Resolverlo En Qanda




中学2年生 数学 式の計算 多項式の計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2数学 項と次数 単項式と多項式の次数の求め方と練習問題 Pikuu




多項式と単項式の違いとは 次数や乗除 乗法除法 や分配法則についても解説 遊ぶ数学



単項式 多項式 何次式 係数 次数の見分け方を解説 数スタ




1研究中 C 数学5 単項式 多項式 整式 分数式 有理式 無理式 係数 項の次数次式元




単項式と多項式 無料で使える中学学習プリント



Studydoctor単項式の係数と次数 高校数学 Studydoctor




どうしてこうなるのかが分かりません 解説お願いします Clear




あの係数って文字も含みますか よく分からないです 数だけじゃないですか Clear




高校 数学 数と式2 係数と次数 10分 Youtube




単項式の次数と係数 Geogebra



Http Www E Net Nara Jp Hs Takatorikokusai Index Cfm 8 763 C Html 763 0507 1005 Pdf




単項式と多項式




高校数学 単項式の係数と次数 映像授業のtry It トライイット




中2 式の計算 単項式と多項式 次数は次の世界を結び付ける 教えたい 人のための 数学講座




文字式 代数式 のルールと単項式 多項式の足し算と引き算 リョースケ大学



単項式と多項式 次数の意味 同類項をまとめる 中学2年数学 式の計算




Left 3right 054 1 1a 1b Descubre Como Resolverlo En Qanda




単項式 多項式と次数 ときどき係数 教遊者




単項式と多項式のそれぞれの意味と違い 数と式




式の計算 単項式と多項式の次数の数え方 中学生からの勉強質問 数学 進研ゼミ中学講座




数学 中2 1 単項式と多項式 Youtube




3分で分かる 単項式とは 単項式とその次数 係数などについてわかりやすく 合格サプリ




多項式と単項式とは 項 次数 係数などの意味や計算問題 受験辞典




中学2年数学 式の計算 単項式と多項式とは その次数と係数もマスターしよう 数学の面白いこと 役に立つことをまとめたサイト



2



数と式の計算問題 まずは公式をしっかり覚えよう 三重の個人契約家庭教師




Kelas 10 Catatan Tentang クルトガ 多項式と単項式 Clear




本当にかっこが多すぎて分からないです 助けてください 教えて欲しいです Clear



次数の意味 単項式 多項式 特定の文字に着目 具体例で学ぶ数学




単項式と多項式の違い 簡単な問題を解けば違いがわかる 中学や高校の数学の計算問題




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ




単項式の係数と次数 着目するポイントはこれだ 中学や高校の数学の計算問題



単項式の次数と係数について 分数の場合の次数と係数の数え方を教えてくだ Yahoo 知恵袋




多項式と単項式の違いとは 次数や乗除 乗法除法 や分配法則についても解説 遊ぶ数学



多項式と単項式とは 項 次数 係数などの意味や計算問題 受験辞典



多項式と単項式とは 項 次数 係数などの意味や計算問題 受験辞典




単項式の次数と係数 数学 A 数と式 Youtube




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ



中2数学 式の計算 単項式と多項式 次数 同類項について たけのこ塾 勉強が苦手な中学生のやる気をのばす




中2数学 単項式と多項式の違い 次数も学べる超簡単な解説 Rikeinvest




単項式 多項式と次数 ときどき係数 教遊者




式の計算 単項式と多項式の違いをマスター 次数に注意 中学数学をはじめから分かりやすく




中学数学2年 単項式と多項式とその次数 受験の月




高校数学 多項式の次数 例題編 映像授業のtry It トライイット




単項式と多項式 高校生 数学のノート Clear




単項式の全てがこれでわかる 単項式の係数と次数 乗法 除法や多項式との違いまで 高校生向け受験応援メディア 受験のミカタ




中学2年数学 式の計算 単項式と多項式とは その次数と係数もマスターしよう 数学の面白いこと 役に立つことをまとめたサイト




数学 多項式の次数と定数項の求め方とコツ 教科書より詳しい高校数学



Www Chofu Schools Jp Chofu7 Otayori Documents 0511 Homework Mathematics2h Pdf



0 件のコメント:
コメントを投稿