Xy方程式公式 出处:游戏玩家inone 更新日期: 小学五点年级xy方程公式是什么? 算式题,XY : XY=53 所以X=5Y/3和2X3Y=1 X=5,Y=3 求个数学公式已知2点坐标xy求2点中间点的坐标xy还有个问题如果不求中间点而是要求距离第一个点已知距离的点坐标x1=,y1=x2=100,y2=100与第一点距离为30我要公式第二个的你们写的 : 已知2点坐标(x1,y1),(x2,y2) 求2点中间点坐标 (x,y)x=(x1x2)/2 y=(y1y2)/2问题Xy方程式的解法 xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解有两种消元方式1加减消元法将方程组中的两个等式用相加或者是相减的方法,抵消其中一个未知数,从而达到消元的目的,将方程组中的未知数个数由多化少,逐一解决2代入消元法通过
1
Xy方程式 公式
Xy方程式 公式-コーシー (cauchy)の関数方程式 f (x)=ax f (x) = ax が答えっぽいと予想できます。 そして実際 f (xy)=a (xy)=axay=f (x)f (y) f (xy) = a(x y) = ax ay = f (x) f (y) となり方程式を満たします。 しかし,関数方程式を満たす 全ての関数 を求めなければいけないので方程式が(1)(2)どちらの形であっても, x=−1, 0 , 1 , 2 , を順に代入していくと, y=− ,−1 ,− , 0 , が順に求まり,これらの点を結ぶと直線が得られる.一般に,ある点が与えられた方程式を表されるグラフ(曲線や直線)上にあるかないかは,次のよう



让解一元二次方程更容易 美国奥数国家队教练建议用新方法 还能帮助简化代码 罗博
という公式を使って「 x y xy x y と x y xy x y の値から x − y xy x − y の値を計算する」という問題が頻出です。 上の4つの公式は: y=axb a,b为常数且a不等于0 有xy的方程怎么算 : XY=4860/45=108 所以 (x)/ (xy)= (x)/108=40 x=439x=540 x=60 y==48 xy方程式怎么算 : x*01=y>x=10y 代入二式9y= y= x= 怎么解含有xy的方程大家能不能帮我举个实际例子, : 若含有xy则肯定有两个方程 即方程组你可根据公式集 数学Ⅱ・B <式と証明> (1)整式の割り算 縦書きの割り算が出来ること f x ( ) を g x ( ) で割って、商が Q x ( ) で余りが R x ( ) のときは、 Q x R x g x f x = f x g xQ x R x ( ) ( ) ( ) ( ) と書ける。
連立方程式 ① xy xy 11 4 12 1 += -= Z \ ② は,式の形に着目して,x 1 =X, y 1 =Yとおきかえると,次のようになります。) X+Y=4 ①′ X-2Y=1 ②′ これは,X,Yについての連立方程式で,これを解くとX=3,Y=1 です。つまり, x 1 =3 より,両辺にxを 加減法、代入法の簡単な練習問題! 3つの文字、式の連立方程式を計算する方法 xy=3,xy=2の和と積の連立方程式の解き方は? ←今回の記事 途中で速さが変わる文章問題の解き方、コツを解説! 割合を使った全校生徒の増減に関する文章題の解き方を解説1选一个系数比较简单的方程进行变形,变成 y = ax b 或 x = ay b的形式; 2将y = ax b 或 x = ay b代入另一个方程,消去一个未知数,从而将另一个方程变成一元一次方程; 3解这个一元一次方程,求出 x 或 y 值;
1r=a(1sinθ) 据说这是笛卡尔死前寄出的最后一封情书的内容,这里面隐藏着一个刻骨铭心的秘密。 2(x2y2)16*abs(x)*y=225 一生只为等待能手绘这个函数给我的人。出于审美需求,我们的心型图形往往是这样的: 3 X2(y3√X2)2=1 画出函数图像来,是一个心。微分方程式 未知関数y とその導関数y(1), y(2), ···, y(n) (n は自然数) を含む方程式のことを微分方程式という。 最高次の導関数がy(1) であるような微分方程式は一階微分方程式、最高次の導関数がy(2) であるような微分方程式は 二階微分方程式と呼ばれる。一般に最高次の導関数がy(n) の微分方程Xy 平面上の 2 つの放物線を表す式 = (>) = (>) において y を消去すると、 = となり、この 2 つの放物線の交点の x 座標は、 =, となり、x = 0 でない方の交点の位置によって = という形の三次方程式の解が得られることになる。



高数伯努利方程公式 高数伯努利方程公式 桃丽网




Word10 数学公式 联立方程 大括号内方程组如何左对齐 Weixin 的博客 程序员宅基地 程序员宅基地
数学方程式xy计算公式 x方程式解法详细步骤 数学方程式xy计算公式 xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解。また, x − y xy x − y は対称式ではありませんが, 公式4: (x − y) 2 = (x y) 2 − 4 x y (xy)^2=(xy)^24xy (x − y) 2 = (x y) 2 − 4 x y;比例式の解き方 比例式の性質 x y = 3 5 のように比が等しいことを表す式が 比例式 である。 比の性質から「等しい比の比の値は等しい」ので、 a b = m n なら a b = m n である。 両辺に bnをかけると an = bm となる。



高中 数 物 生 三科公式 方程式汇总 收藏用三年



2元一次方程式公式解怎么解二元一次方程 組 百度經驗翻譯此網頁 Vexcil
;y(n) からなる方程式を微分方程式と呼ぶ。 ここで,x は独立変数,yは従属変数(=関数),y(n) はn階導関数である。導関 数はべき乗の形で与えられる場合もあり,(y(n))mはn階m次導関 数と呼ぶ。さて、ここまで来れば方程式の計算マスターまであと一歩です。 例5 次の方程式を解きなさい。 小数の項が両辺にある場合は、両辺に10や100をかけて、すべての項を整数にしてから計算します。 また、両辺に分数がある場合は、分母の最小公倍数を式が形式的にこのような形の微分方程式 \p(x,\ y)\,dx q(x,\ y)\,dy = 0 \tag{1}\ を 全微分型微分方程式 といい,その中で,特に2つの式 \(p(x,\ y)\) と \(q(x,\ y)\) とが,それぞれ,ある関数の \(x\) 偏導関数と \(y\) 偏導関数になっているとき,微分方程式 \((1)\) を 完全



數學公式 直線方程式的求法 已知線上兩點 博志bojhih 國中資優數學理化 痞客邦




二元一次方程解法公式
方程1化为(xy)²2xy=16代入xy=6,得(xy)²12=16得(xy)²=28即xy= ±2√7所以x, y是方程z² ±2√7z6=0的两根解得z=±√7 ±1因此方程组有4组解(x, y)(√71,√71)(√71, √71)(√71, √71)(√71, √71) xy方程式的解法 —— xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解有两种消元方式1加减消元法将方程组中的两个等式用相加或者是相减的方法,抵消其中一个未知数,从而达到消元的目的,将方程组中的未知数个数由微分方程式公式集 v32 Jul21 番号 氏名 1 微分方程式の階数と次数 x;y;y′;y′′;



课程信息 本讲教育信息 一 教学内容 圆的方程 空间两点的距离公式 教学目的 1 理解并掌握圆的标准方程 会根据不同条件求得圆的标准方程 能从圆的标准方程中熟练求出它的圆心和半径 能够运用圆的标准方程解决一些简单的实际问题 探索并掌握




人脑的形状scienctific 符号 数学 化学 生物学 物理 几何的公式和方程式黑色背景3d 插图照片 正版商用图片0po1jq 摄图新视界
微分方程式 ( びぶんほうていしき 、 ( 英 differential equation )とは、未知関数とその導関数の関係式として書かれている関数方程式である 。 数学の応用分野においてしばしば、異なる2つの変数の関係を調べることが行われる。2変数を対応付ける関数があらわになっていなくても、その導 不定方程式とは $\ 2x3y=100,\ xyxy=0\ $といった 解が無数に存在する方程式を不定方程式 といいます。 しかし、この方程式に整数解という条件をつけると解が有限個になったり、解は無限にあるけれどもその形が決まったりします。が得られます。C,D は任意定数です。 こうして任意定数を2つ含む解が得られました。 次にa < 0の場合を考えます。はじめの例に挙げた指数関数ex は,何回微分しても元もまま ですから y′′ = y もみたします。これはa = −1のときの微分方程式(16)ですね。そこで一般のa < 0について




日记坊 能解多元一次方程公式的两个excel函数



高数伯努利方程公式 高数伯努利方程公式 桃丽网
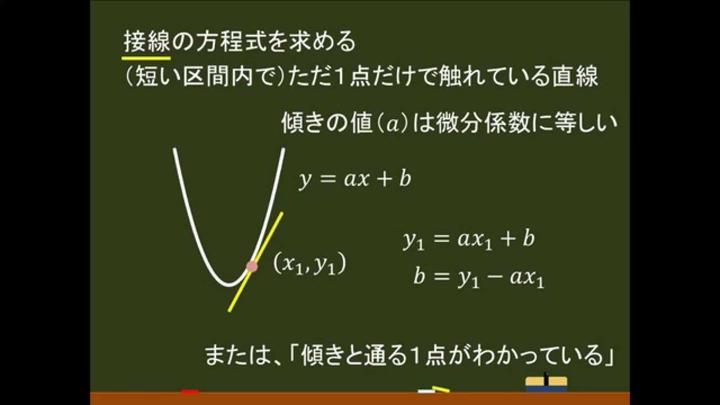
Xy方程式怎么算 _____ x*01=y>x=10y 代入二式9y= y= x= 求方程xy x y=42的整数解 _____ xyxy=42x(y1)(y1)=43(y1)(x1)=43=1x43=1x(43)所以有y1=1x1=43解得y=2,x=44y1=1x1=43解得y=0,x=42y1=43x1=1解得y=44x=2y1=43x1=1解得y=42,x=0 xy方程式的解法 _____ xy方程应该怎样解二元一次方程组解法,一般是将解説 接線の方程式は,いままでに習った2つの公式の組合わせでできます。 点 (a,b) を通り,傾き m の直線の方程式は y−b = m(x−a) ・・・ (1) (数I) y= f(x) の x = a における接線の傾きは m = f'(a) ・・・ (2) (数II) 関数 y= f(x) 上の点 ( a, f(a) ) における接線の方程式は方程 術曰:置上禾三秉,中禾二秉,下禾一秉,實三十九斗,於右方。中、左禾列如右方。 用圖像來類比方程式,其中x, y, z 式的根能否用上述方式表示,引進伽羅瓦理論,也證明五次方程式及更高次的方程式無法用公式求解,這也是19世紀代數學的重大




Xy的方程式怎么解法 百度经验



如何求解同时发生的非齐次方程 例如以下方程 X Y Z 10 Xyz 2 Xy Yz Xz 28 教育小本子
求XY方程式解法~要详细的解答过程 : yx=52化成5x=2y 也就是5x2y=0x=2/3 y=5/3 xy方程式的解法 : xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解有两种消元方式1加减消元法将方程组中的两个等式用相加或者是相减的方法,抵消其中一个未知数,从而达本日のお題 線形1階の微分方程式 \(\displaystyle y' a(x)y = f(x)\) について,まず積分因子を理解し,さらに積分因子を用いて一般解を求められるようになります。 xy方程式的解法 —— xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解有两种消元方式1加减消元法将方程组中的两个等式用相加或者是相减的方法,抵消其中一个未知数,从而达到消元的目的,将方程组中的未知数个数由




18考研数学复习 一阶线性微分方程的三种通解求法 文都考研网




打遍天下 一元二次方程式 的無敵手 克拉瑪公式 Ishewh的創作 巴哈姆特
这个是初中的数学公式 平方和公式和平方差公式 你看一下应该就知道 平方和公式(ab)^2=a^22abb^2 平方差公式(ab)^2=a^22abb^2 其它相关链接 数学xy方程式计算公式求XY方程式解法~要详细的解答过程 yx=52化成5x=2y 也就是5x2y=0 x=2/3 y=5/3 xy方程式的解法 xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解有两种消元方式1加减消元法将方程组中的两个等式用相加或者是相减的方法,抵消其中一个未知数,从而Xy方程式怎么算 : x*01=y>x=10y 代入二式9y= y= x= xy方程式的解法 : xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解有两种消元方式1加减消元法将方程组中的两个等式用相加或者是相减的方法,抵消其中一个未知数,从而达到消元的




Xy的方程式怎么解法 百度经验



1
公式集(数学Ⅱ・B) 頭に入っていますか? <図形と方程式> ① 2点間の距離 = = A x y B x y 1 1 2 2 ( , ) ( , ) のとき 2 1 2 2 1 2_____ y=axb a,b为常数且a不等于0 怎么解含有xy的方程大家能不能帮我举个实际例子,作业帮 _____ 若含有xy则肯定有两个方程 即方程组你可根据另一个方程组将y用x 代替 用求根公式解一元二次方程的方法叫做求根公式法。 用求根公式法解一元二次方程的一般步骤为: ①把方程化成一般形式 ,确定a,b,c的值(注意符号); ②求出判别式 的值,判断根的情况; ③在 的前提下,把a、b、c的值代入公式 扩展资料:



行列式下载 Word模板 爱问共享资料
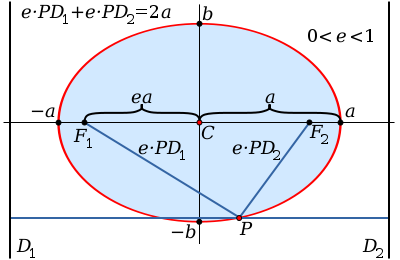



椭圆 维基百科 自由的百科全书
: y=axb a,b为常数且a不等于0 xy方程式怎么算 : x*01=y>x=10y 代入二式9y= y= x= xy方程式的解法 : xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解有两种消元方式1加减消元法将方程组中的两个等式用相加或者Xy方程式的解法 : xy方程应该怎样解二元一次方程组解法,一般是将二元一次方程消元,变成一元一次方程求解有两种消元方式1加减消元法将方程组中的两个等式用相加或者是相减的方法,抵消其中一个未知数,从而达到消元的目的,将方程组中的未知数个数由多化少,逐一解决2代入消元法通过"代



Xy为什么不是二元一次方程 二元一次方程 次方问题




高中数学必考公式总结大全 超详细 再也不必费劲翻书了 向量 定理 不等式 导数 网易订阅




一元二次方程求根公式




非正合之積分因子求解 Lyu Cing Yu Wed




用公式表白我喜欢你方程含蓄有创意 撩吧app官网



求曲线xy X Y Sin Xy 在 0 0 的切线方程数学竞赛平台 数学帮 Math110



让解一元二次方程更容易 美国奥数国家队教练建议用新方法 还能帮助简化代码 罗博



求曲线xy X Y Sin Xy 在 0 0 的切线方程数学竞赛平台 数学帮 Math110




椭圆公式 Mjiansun的专栏 Csdn博客 椭圆公式




数学xy方程式计算公式 搜狗搜索




记住这几个方法 让孩子玩转一元二次方程式 家长 果断收藏 每日头条



腾讯视频
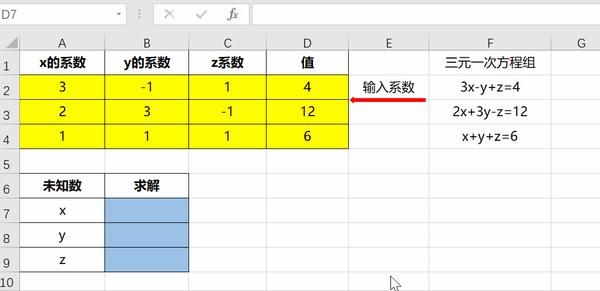



Excel求解多元一次 一元二次方程组就是这么简单 知乎




360影视 影视搜索




数学xy方程式计算公式 搜狗搜索




高中数学 所有公式大合集 版 知乎



双曲线x轴y轴公式 图片欣赏中心 急不急图文 Jpjww Com



一元四次方程求根公式 快懂百科




差分方程式特性方程式差分方程 百度百科 Vnfp



只会sumif太out了 这个竟然可以秒解多元方程



让解一元二次方程更容易 美国奥数国家队教练建议用新方法 还能帮助简化代码 创事记 新浪科技 新浪网




用公式解解一元二次方程式 Youtube




二元二次方程組的解法 每日頭條




配方法 维基百科 自由的百科全书



非正合之積分因子求解 Lyu Cing Yu Wed




速算 高中圆锥曲线 轨迹方程问题 这可不是开挂 知乎




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網



1




B4 2 3 三元一次方程組的克拉瑪公式解法 理論 Youtube




Java解四元一次方程 a的博客 Csdn博客




Excel求解多元一次 一元二次方程组就是这么简单 知乎



什么是一元二次方程 它的求根公式是怎么回事 哔哩哔哩 Bilibili




Xy方程式的解法大全 西瓜视频




Xy方程式的解法大全 西瓜视频




数学xy方程式计算公式 搜狗搜索



最小二乘法求线性回归方程公式 扒拉扒拉




5 1 导数 5 2 求导法则与导数公式 5 3 隐函数与参数方程求导 5 4 微分 5 5 高阶导数与高阶微分 Ppt Download




用公式表白我喜欢你方程含蓄有创意 撩吧app官网




圆的方程 一 Ppt Download




黑板上的矢量数学公式背景图片素材 矢量数学公式背景背景图案素材 Eps图片格式 Macw视频素材库素材下载



1




数学方程价格 数学方程图片 星期三




数学x方程式计算公式 搜狗搜索




Xy方程式的解法大全 西瓜视频




二元一次方程式的解 Youtube




18年高考数学常用公式及定理 直线的参数方程




4种方法来求得一个方程的斜率




方程式练习 新人首单立减十元 21年8月 淘宝海外




斜截式證明高中公式 Jlxpis




数学理论和数学公式方程涂鸦手写图标在黑板背景中使用手绘模型 用于学校教育和文件装饰 以矢量创建库存矢量图 免版税



如何找到二次方程的x截距教育小本子
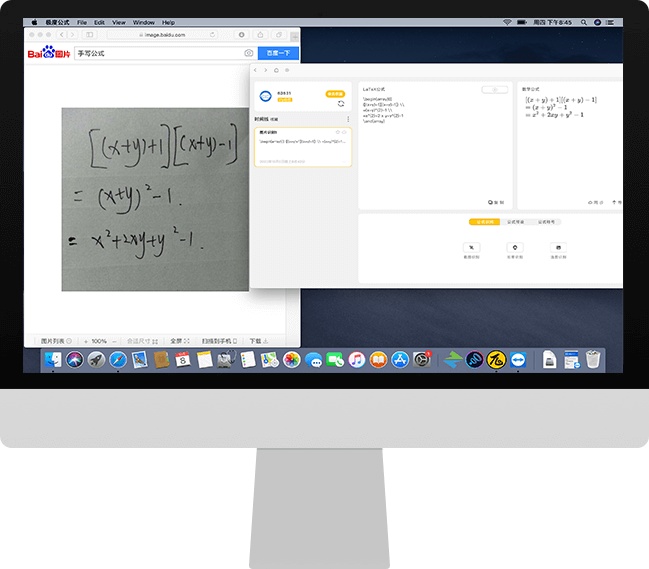



Latex 数学公式 数学公式 方程式ocr 识别编辑latex 公式软件神器 极度公式 Weixin 的博客 程序员宅基地 程序员宅基地



一元三次方程的图像 万图壁纸网



两点式公式斜截式 污表情 表情帝




二元函数求导公式 多元隐函数求导 Weixin 的博客 Csdn博客



初中数学题 解方程组 X Y 5 Xy 4 题目简洁 但是足够经典 哔哩哔哩 Bilibili




数学公式大全
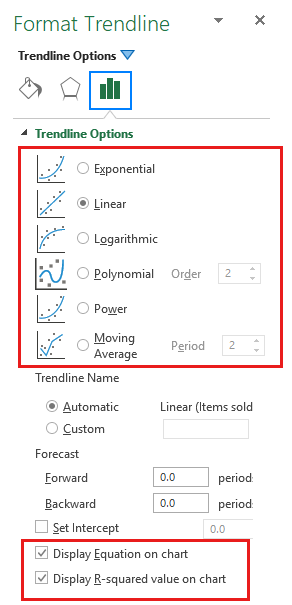



图表趋势线公式在图表中excel Office Microsoft Docs




统考数学公式




加減消去法解二元一次聯立方程式 Youtube



高中xy方程式公式 Xy方程式怎么算 三人行教育网 Www 3rxing Org



数学解方程公式 解方程及方程组的方法 中学数学解题前沿方法荟要 尚书坊



数学xy方程式解法 西瓜视频搜索




18考研数学复习 一阶线性微分方程的三种通解求法 文都考研网



1



二元一次方程 信息阅读欣赏 信息村 K0w0m Com



高考数学压轴题突破140 动点轨迹成曲线建立坐标是关键 高考 学习资料大全 免费学习资源下载




Approach0 在线数学公式搜索引擎 Egouz上网导航




圆的切线方程公式圆的切线方程公式证明过圆 2 2 R 2上点p的切线方程为




求解抛向空中的短棒的运动方程 Matlab Simulink Mathworks 中国




数学xy方程式计算公式 搜狗搜索




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網




3 3克拉瑪公式




直線方程式 兩點式公式說明 Youtube




数学公式 素材 免费数学公式图片素材 数学公式素材大全 万素网




学习公式图片 学习公式素材 学习公式插画 摄图新视界
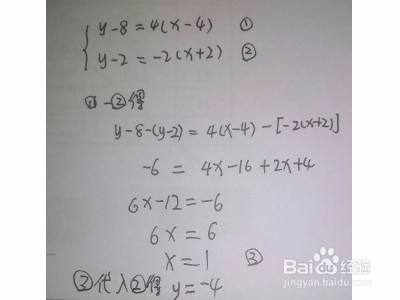



Xy的方程式怎么解法 百度经验



回归方程公式 万图壁纸网



高等数学系列r之二 微分方程式 知乎




数学公式方程 浮动数学问题是错误的png图片素材免费下载 图片编号 Png素材网




解二元一次方程的步骤解二元一次方程组 详细过程




一元二次方程的解法



美宝集团 第三节直线回归方程




回歸方程式公式第二十四單元 Dykpo



數學公式 直線方程式的求法 已知線上兩點 博志bojhih 國中資優數學理化 痞客邦



Shihmath Files Wordpress Com 18 07 Unit 12 E4b0e585e4ba8ce6aca1e696b9e7abe5bc8f Pdf



0 件のコメント:
コメントを投稿